關於數字的秘密含義歷來一直都有很多猜想。縱使確實有不少令人驚艷的發現,但可以肯定的是,隨著畢達哥拉斯長眠不起,這門科學的奧義已經一去不復返了。近兩千五百年來的所有民族的哲學家都試圖解開畢達哥拉斯學派留下的謎團,但顯然其中無一人成功。儘管有人企圖抹除畢達哥拉斯的教誨的所有記載,但仍有些片段成了得以倖免於難,這些為他哲學中的一些較為簡單的部分提供了線索。最主要的奧祕從未被書寫下來,不過至少有被口頭傳授給少數的幾個門徒。這些人顯然也無意讓他們的奧祕遭到褻瀆,於是乎,當死亡永遠地封住他們的嘴巴的時候,奧祕也跟著他們一同重歸塵土。
在今天仍有某些秘密學院是古代神秘學派的繼承者,即使它們可能握有一些原始的數學公式,但從這些團體在過去五百年來發表的海量著作中卻沒有證據顯示確實如此。這些著作儘管經常論及畢達哥拉斯,可是對於他那一言難盡的教義,它們卻似乎不比畢氏之後的希臘猜測者要懂得更多,那些猜測者也是談得很多、寫得很少、知道得更少,根本是在用一系列故弄玄虛的暗示和承諾中來掩藏他們的無知。在早期作家的作品裡不時可以發現神秘朦朧的字句,他們也幾乎不費吹灰之力在去為其作出解釋。下面的例子引自普魯塔克:
“畢達哥拉斯學派確實走得更遠,它們更以諸神的名字與頭銜來榮耀雙數和幾何圖形。故此,它們稱等邊三角形叫頭生的密涅瓦跟特里托格內亞(Tritogenia),因為它可以被依每個角的三條垂直線均分。所以他們稱呼單數為阿波羅,數字2被貼上了爭鬥與大膽之名,數字3則是正義。就如同傷害者是一個極端,受傷害者是另一個極端,痛苦介於其中間。就像它們的數字三十六,聖十三角形或神聖的四元數(Quaternion),由頭四個單數和頭四個雙數組成,如過去常記載,它們認為這就是最莊重的誓言,名作宇宙(Kosmos)。”(參見《伊西斯與奧西里斯》)
在同一本著作的更前面,普魯塔克也提到:
“因為三角形的力量展示出了普路托、巴克斯以及馬爾斯的本性;正方形的特性屬於瑞亞、維納斯、刻瑞斯、維斯塔和朱諾;十二面體是朱庇特;所以,就像我們從歐多克索斯那獲悉的,五十六角形盡顯了堤豐的本質。”
普魯塔克並沒有假意去解釋這些象徵的深意,他只是相信畢達哥拉斯之所以在幾何圖形與諸神間建立聯繫,其實是這位聖賢在埃及神殿裡曾所聞過的結果。
偉大的共濟會象徵主義者艾伯特・派克承認在這方面他也愛莫能助。在他為32-33級成員所寫的《象徵主義》中,他就寫道:“我不明白數字7為什麼會被稱為密涅瓦,或立方體和涅普頓。”他還繼續補充說:“毫無疑問,被畢達哥拉斯賦予給不同數字的各個名字本身就極具神秘和象徵性,而且這些名字的含義很明顯在普魯塔克的時代都已經遺失。畢達哥拉斯實在用那無法穿透的面紗把自己的象徵符號隱瞞得太出色了,他從不作任何口頭解釋。”
所有真正在鑽研這個主題的學生都會對這種困惑之感深感認同,他們實在地證明了,要想根據關於畢達哥拉斯學派的數學哲學體系的殘缺不全的信息來妄下斷言著實極為不智。下面的材料是畢達哥拉斯的門徒以及其他曾學習過他的哲學的人努力從一盤散沙的記錄中搜集的成果。
確保單詞的數字力量的方法
要獲得一個單詞確切的數值得要做的第一步就是要把它還原回最初的語言。只有派生自希臘文和希伯來文的單詞可以透過這種方式進行解析,而且所有單詞都必須被溯源至它們最古老且完整的模樣。因此,出現在《舊約》裡的單詞跟名字得要被翻譯回早期的希伯來文,《新約》則是希臘文。列舉這兩個例子也有助於說明這一原則。
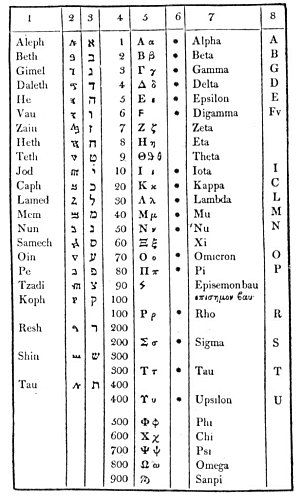
猶太人的德謬歌就是英文中的耶和華,但如果要發掘耶和華這個名字的等值數值,就需要將這個名字還原成希伯來文。如此它就會變成יהוה,要從右向左讀。這些希伯來字母分別是:ה, He; ו, Vau; ה, He; י, Yod,當按照英文時則要從左向右讀:Yod-He-Vau-He。經過查閱字母數值表,我們可以發現這個聖名的四個字各具有下列數值意義:Yod等於10、He等於5、Vau等於6,然後第二個He也等於5。所以10+5+6+5=26,這就是耶和華的同義值。假使用的是英文字母,那答案顯然就不會正確。
第二個例子是神秘的諾斯底神祇阿巴薩克斯,將為這個名字派上用場的是希臘文字表。阿巴薩克斯的希臘文是Ἀβραξας. ,Α = 1, β = 2, ρ = 100, α = 1, ξ =60, α = 1, ς = 200,總和為365,相當於一年的天數。這個數字就為破解阿巴薩克斯的奧祕提供了鑰匙,他是三百六十五個移湧(Aeons)或歲月之靈(Spirits of the Days)的象徵,它們聚合而成了一個複合人格。阿巴薩克斯也是五種生物的象徵,而一年的循環圈實際上有三百六十度,從中發散而出的神靈各代表這股力量的五分之一,即七十二,這是猶太人的《舊約》及卡巴拉體系中最神聖的數字之一。同樣的這套方法也可被用於尋找希臘人和猶太人的男神與女神的名字數值。
所有更大的數字都可以被化約為最基本的十個數字,數字10也可直接被減約為1。所以,所有翻譯自這些神祇的名字的數值皆可轉換成頭十個數字的相應值。根據這套系統,通過把每個數字加總在一起,666就會變成6+6+6=18,然後它又能變為1+8或9。據《啟示錄》記載,未來將有十四萬四千人被揀選。一旦把這個數字化為1+4+4+0+0+0,即得9,從而證明巴比倫大淫婦和被揀選的人其實都是在隱喻人自己,其象徵數字就是9。無論是希臘文還是希伯來文字母值,這套系統都管用。
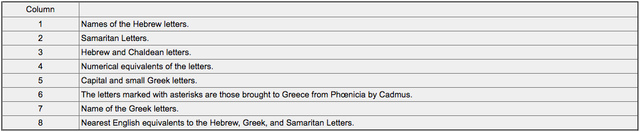
希伯來、希臘和撒馬利亞字母數值表,引自希金斯《凱爾特的德魯伊》。
請注意:當被寫在詞末時,希伯來文的Tau的數值為440、Caph是500、Mem是600、Nun是700、Pe是800、Tzadi 是900。有點的Alpha和虛線的Aleph的數值為1000。
原來的畢達哥拉斯數學哲學系統完全無意證明,時下很流行的那種想靠改名改姓來改變脾性或財運的做法有任何可取之處。
英文也有一個流行的換算系統,但它的實用性一直充滿爭議。它更為晚近、且與希伯來卡巴拉體系或希臘體系沒有任何瓜葛。有些人認為沒有任何實質證據可以證明它來源於畢達哥拉斯學派,而且與之相應的論據也有不少。畢達哥拉斯使用10作為計算基礎,但這套系統卻是使用9——這是一個代表不完美的數字——光是這點就已是決定性的。另外,希臘文和希伯來文的字母編排也與英文不盡能相對照,所以並不應該把其中一門語言的數值直接拿來與其它比較。
對這套系統的深入實驗也許能證明它的合用性,但起碼它沒有任何古代根據。這套字母和數字的對照如下:
位於下方的字母都與表格頂端的數字對應。因此,在人(man)這個單詞中,M=4、A=1、N=5:總和即為10。這些數值幾乎與畢達哥拉斯學派的體系相同。
畢達哥拉斯學派的數學理論的概述
(以下對畢達哥拉斯學派的數學的介紹是對托馬斯・泰勒的《算術理論》〔Theoretic Arithmetic〕開頭一章的解讀,那本書彙編了現存最稀有且重要的畢達哥拉學派的數學片簡)
畢達哥拉斯學派宣稱算數是數學科學之母。事實的確證明無論是幾何、音樂或天文都要依賴於它,但它卻不必一定要依賴它們。所以即使幾何可能被棄置,不過算術依舊常在;但假使被拋棄的是算術,那麼幾何也無法復存。音樂也以同樣的方式決繫於算術,但抹除音樂則只會由於它的其中一種表達形式受限制從而影響算術。畢達哥拉斯學派還堅持算術先於天文學,因為後者又同時依賴於幾何與音樂。天體的大小、形狀跟運動都是由幾何學決定;它們的和諧與節奏亦都是音樂的運用。如果天文學被罷黜,那對幾何學和音樂並不會有什麼損失;但如果罷黜的是幾何學和音樂,天文學就會損失甚重。幾何與音樂正是出於這個原因才優先於天文,然而算術卻更在它們所有之前;它是最首要且基本的。
據畢達哥拉斯教導他的門徒,數學科學可以被分成兩個主要部分。第一個部分涉及數量(multitude)或事物的組成部份,第二個部分涉關大小(magnitude)或事物的相對大小或密度。
大小又可再分為兩部分——固定的大小和可變的大小,其中以固定的為先。數量同樣也有兩部分,因為它既與自身也與其它事物有關聯,為先的亦是頭一種關聯。畢達哥拉斯將算術科學分配給與自身相關的數量,音樂技藝則被分配給與其它事物相關的數量。幾何被分配給固定的大小,而球體(部分用於天文學)屬於可變的大小。無論是數量還是大小,都會被心智的圓周所限制。原子理論現在已經證明大小是數量的結果,因為質量本身是由無數微小的單元組成,儘管其常常被誤以為是單一的物質。
礙於畢達哥拉斯學派的材料所剩不多,要確切地釐清各種術語並不容易。然而,在進一步討論下去之前,必須先把目光聚焦到數字、單子以及一(one)這些單詞的含義。單子的含義有(a)涵蓋一切的太ㄧ。畢達哥拉斯學派讚譽單子是“高貴的數,諸神與人的祖先”(b)被視之為一個整體的任何數字組合之總和。因此,宇宙被認為是一個單子,但宇宙中的各個部分(譬如行星與元素)卻也是相關於它們自身組成部份的單子,當然它們都是構成它們的總和的更大單子的一部分。單子同時也可以被比擬為(c)一棵茁壯茂盛、開枝散葉(數字)的樹的種子。換句話說,這些數字就是樹枝之於樹種子的單子。透過對畢達哥拉斯學派神秘的單子的研究,萊布尼茲提出了他宏偉的世界原子理論——這個理論完全符合神秘學派的古老教義,畢竟萊布尼茲自己就是一間秘密學院的創辦人。對於一些畢達哥拉斯學派的人來說,單子也可以被看作是(d)ㄧ的同義詞。
數(Number)是一個適用於所有數字及其組合的術語(某些畢達哥拉斯主義者對數的嚴格解釋並不包括數字1和2在內)。畢達哥拉斯將數字定義為包含著單子的孕育因(spermatic reasons)的延伸與能量。希帕索斯的追隨者還聲稱,數字就是德謬歌在創造宇宙時所按照的第一種範式。ㄧ被柏拉圖主義者定義為“眾多的首先”。不同於單子的是,前者是被用於描述一個單元的部分之總和,但一卻是用來指稱它的每ㄧ個完整部分。
數字本身也沿循著兩種秩序:奇數與偶數。由於統一數或數字1總是不可分割的,所以奇數也不能被均分。所以9=4+1+4,這個統一數的中心已不能再分割。除此以外,如果把奇數再分為兩部分,其中一部分便將永遠是奇數,另一部分永遠是偶數。故9也可以被=5+4、3+6、7+2或8+1。畢達哥拉斯學派相信奇數——以單子作為原型的這種數——是確切且屬陽性的。不過它們都並不匹配於統一數或數字1的本質。有些人聲稱它是積極的,因為如果添加偶數(消極)進去,就又會產生出另一個奇數(積極)。也有其他人認為如果為統一數加上偶數,後者就會因而變成可被均分,這就是使得陽性變成陰性。所以統一數或數字1被視作為一個雌雄同體的數字,同時兼具男性與女性的特徵;也就是有奇數又有偶數。基於這個理由,畢達哥拉斯學派稱它是奇數。畢達哥拉斯學派就是因此才習慣於向高級的神祇獻上數量不均的供物,獻給女神和地下神靈的則是選擇可均分的偶數。
任何偶數皆可被拆分為兩個相等部分,它們總是或者都是奇數或都是偶數。10=5+5,兩者都是奇數。哪怕10被不均等地拆開,同樣的原理也萬殊一撤。例如6+4這兩者皆為偶數;7+3兩者都是奇數,8+2兩者都可被均分,然後在9+1中又都是奇數。所以在可被拆分的偶數中的部分要不全都是奇數就都是偶數。畢達哥拉斯學派認為偶數的原型是成對(duad)——即是不明確且陰性化的。
奇數能被通過數學構思來再分——這又被稱作埃拉托斯特尼篩法(Sieve of Eratosthenes)——它可以劃分出三個類別:質數、合數以及無公因數。
質數是那些除它們自己以及統一數之外都不能被除盡的數,例如3、5、7、11、13、17、19、23、29、31、37、41、43、47。像7就只能被7整除,它只能自除一次,但如果是用統一數卻可以有七倍。合數是那些不只可以被自身與統一數,而且還能被其它數字整除的數,例如9、15、21、25、27、33、39、45、51、57等等。21不僅能被自身跟統ㄧ數整除,也可以被3和7除盡。
無公因數就是那些沒有公因數的數,儘管它們都還能被再分,譬如9與25。舉例來說,9可以被3整除,25也可以被5整除,但彼此都不能被彼此的除數整除;因此它們並無共同因數。由於它們各有各自的因數,所以它們可被稱為合數,但又因為它們沒有共同因數,因此術語無公因數就被發明來描述它們的性質。
偶數亦能被分為三類:能分偶數、能分奇數、奇奇數。任何能分偶數都是統一數的雙倍比例,比如:1、2、4、8、16、32、64、128、256、512、1024。一個完美的能分偶數的證明就是它可以被減半,然後它的半數又能被繼續減半,正如64的1/2 = 32、32的1/2 = 16、16的1/2 = 8、8的1/2 = 4、4的1/2 = 2、2的1/2 = 1;唯獨統一數是最終不可超越的壁障。可分偶數還具備另一種特質,那就是每個數目中的數字總和總是等於最後一項減一。舉個例子:數目第一項和第二項(1+2)之和等於第三項(4)減一;或是第一項、第二項、第三項、第四項(1+2+4+8)之和等於第五項(16)減一。
在一系列能分偶數中,第一項乘以最後一項必等於最後一項,第二項乘以倒數第二項也必等於最後一項,依此類推直到在一個序列中的奇數與最尾末的數相乘;或是在偶序列中的兩個數字,它們彼此相乘也能得出最後的數字。打比方:1、2、4、8、16就是一個奇序列。第一個數字(1)乘以最後一個數字(16)仍等於最後一個數字(16)。第二個數字(2)乘以倒數第二個數字(8)等於最後一個數字(16)。作為奇序列,4位在中心,而且它自己乘自己也等於最後一個數字(16)。
能分奇數是減半時就無法再減半的數字。它們是由按序排列的奇數乘以2後形成,按照這個編排,奇數1、3、5、7、9、11就會產生出能分奇數,2、6、10、14、18、22。因此,每個四項數都是能分奇數。每一個能分奇數皆可被分約一次,如2可以變成兩個1但就無法再被分下去;或6也可以變成兩個3但也得就此止步。
埃拉托斯特尼篩法,引自托馬斯・泰勒《算術理論》。
這個篩選法是被埃拉托斯特尼發明於約公元前230年左右的數學策略。一旦掌握其理論,就可以非常容易地運用。所有的奇數首先都會按照它們的自然順序排列,ㄧ如呈現在圖中底部第二面的指定奇數。接著可以注意到,每第三項數(始於3)都能被3整除、第五項數(始於5)都能被5整除、第七項數(始於7)都能被7整除、第九項數(始於9)都能被9整除、每十一項數(始於11)都能被11整除,依此類推至無窮無盡。這套系統最終淘汰了畢達哥拉斯學派的所謂“質數”,或是除自身和統一數之外都沒有除數的數字。這些數字可以在圖中下層的區域找到,就是指定的首數和合數。據大衛・尤金・史密斯(David Eugene Smith)在他的《數學的歷史》(History of Mathematics)中指出,埃拉托斯特尼是亞歷山卓最偉大的學者之一,甚至被他的崇拜者尊為“第二柏拉圖”。埃拉托斯特尼曾在雅典接受教育,除了因篩法聞名,他還曾通過非常巧妙地方法來計算地球的周長與直徑。他對地球直徑的估算只比現代科學家公認的極徑(polar diameter)少了五十英里。埃拉托斯特尼的這個以及其它數學成就無不令人信服地表明,在基督降生之前的前第三世紀,希臘人不僅知道地球是球形,而且還能夠以極其驚人的準確度來估算其實際尺寸和它同太陽、月亮的距離。另一位偉大的希臘天文學兼數學家,薩摩斯島的阿里斯塔克斯生活在公元前250年左右,他透過哲學演繹和ㄧ些簡單的科學手段斷定應該是地球繞著太陽轉才對。儘管哥白尼深信自己是此一事實的發現者,但他其實是重申了阿里斯塔克斯在一千七百年前的發現。
能分奇數的另一個特點是如果除數是奇數,那商就往往會是偶數,而且假如除數是偶數,那商就會是奇數。例如:18÷2(偶數除數)商得9(奇數)、18÷3(其數除數)商得6(偶數)。
能分奇數還有一點相當醒目,即它兩邊之項的總和總是等於其本身的一半。舉例來說:
10是6和14總和的一半、18是14和22總和的一半、6是2和10總和的一半。
奇奇數或不能分偶數是能分偶數和能分奇數之間的折衷數。不同於能分偶數,它們不能被減半回統ㄧ數;也不同於能分奇數的是,它們能經由減半來得出不止一次分法。奇奇數就是得自把2以上的能分偶數乘以1以上的奇數,大於1的奇數有3、5、7、9、11等等,大於2的能分偶數則有4、8、16、32、64等等。將這個序列的第一個奇數(3)乘以4(序列的第一個能分偶數)就會得到12,第一個奇奇數。通過將5、7、9、11及其之後的數字乘以4,就可以繼續推演出此後的奇奇數。只要繼續乘起3、5、7、9、11和其它,或是反過來說的其它能分偶數(8、16、32、64等)就可以獲得其它奇奇數。把奇奇數減半的例子如下:12的1/2=6、6的1/2=3,由於畢達哥拉斯學派不會再分割統一數,所以接下來就不能繼續減半下去。
偶數本身也能夠分為三類:豐數、虧數與完全數。
超完全數或豐數是指那些自身各個部分的總和會大於它的數字。例如:24的1/2=12、1/4=6、1/3=8、1/6=4、1/12=2和1/24=1。這些部分(12+6+8+4+2+1)的總和為33,它顯然大於原來的24。
虧數是那些自身各個部分的總和小於它的數字。例如:14的1/2=7、1/7=2、1/14=1。這些部分(7+2+1)的總和為10,小於原來的14。
完全數是那些自身各個部分的總和等於它的數字。例如:28的1/2=14、1/4=7、1/7=4、1/14=2和1/28=1。這些部分(14+7+4+2+1)的總和等於28。
完全數非常罕見。在1-10中只有一個,那就是6、10-100中也只有一個,那就是28、100-1000中有一個,那就是496、1000-10000中有一個,那就是8128。要找出完全數可以經由下列的規則:先把能分偶數序列(1、2、4、8、16、32等)的第一個數字與第二個數字相加,然後再將如此得出的合數乘以相加得出該合數的能分偶數序列的最後一個數字。這個結果就是第一個完全數。譬如:第一和第二個能分偶數分別是1跟2。它們的總和是3,這是一個合數。如果讓3乘以2,亦即該能分偶數序列的最後一位數的話,那麼就會得到6,第一個完全數。如若相加的能分偶數沒辦法得出合數,那麼就必須在能分偶數序列中繼續相加直到有了合數為止。第二個完全數可以依照下列規律找到:能分偶數1、2、4之和為7,這就是一個合數。如果7乘以4(得出它的該能分偶數序列最後一位數)就可以得到28,第二個完全數。這套計算方法可以繼續套用至無窮大。
完全數乘以2就會得出豐數,除以2則會得出虧數。
畢達哥拉斯學派是從數學科學中發展出了它們的哲學,下面這個引用自《算術理論》的段落就是一個很好的例子:
“因此,完全數就成了介於過多與缺乏之間的美德的美麗映像,而不是像某些古人認為的代表巔峰。一種邪惡亦會反對另一種邪惡,但兩者都一樣抵觸善良。然而,善良卻從不會反對善良,而是一起對付兩種邪惡。因此膽小雖與大膽相反,但這兩者都是缺乏真正勇氣的人所共有的;而且膽小與大膽也都和堅韌相反。詭計與昏庸相反,但兩者都是缺乏智慧的人所共有的;而且兩者亦都和謹慎相反。同理,貪婪也反對貪婪,兩者都共有吝嗇;同時也都反對寬宏。這個情形在其它美德方面也相去不遠;顯然完全數皆與這些美德有很大的相似性。它們在另一方面也很類似於美德;它們非常少見,而且是生成自相當穩定的秩序。反之,無限多的豐數和虧數總是屢見不鮮,又不具任何有序的傾向,也不是生成自哪一端;因而它們與繁多、複雜且不定的惡(vices)更為相像。”
十個數字表
(下面對於畢達哥拉斯學派的數學的概述是摘自尼科馬庫斯、士麥那的泰昂、普羅克洛、波爾斐利、普魯塔克、亞歷山卓的革利免、亞里斯多德還有其他早期權威的著作)
單子——數字1——會被這麼稱呼是因為它總是處於相同的狀態——換言之就是不同於眾多。它的屬性大致如下:它被稱為心智,因為心智是穩定且具有最優越地位的、它被稱為雌雄同體,因為它既是男性又是女性、它被稱為奇數和偶數,因為它被加至偶數時就可使之變成奇數,加至奇數時就可使之變成偶數、它被稱為上帝,因為它是一切的開始也是結束、它被稱為善,因為這是上帝的本性、它亦被稱為物質的容器,因為它產生了作為物質實質的雙數。
畢達哥拉斯學派也將單子稱作混沌、朦朧、裂口、塔耳塔洛斯、斯提克斯(Styx)、深淵、忘卻之河(Lethe)、阿特拉斯、軸心、摩爾芙(Morpho)以及朱庇特之塔或王座,因為它是存在於宇宙中心的巨大力量,並控制著關於其自身的刨床圓周運動。單子還被稱為苗種因(germinal reason),蓋因它是宇宙間所有思想的起源。還有其他名稱也被賦予給它:阿波羅,這是出於它與太陽的關係、普羅米修斯,因為他為眾人帶來光明、腓力俄斯(Pyralios),他是一個生活在火中的人、誕生(geniture),因為沒有它便無ㄧ數字可存、物質,因為物質是首要的、真理的原因和交響樂的構造,這也同樣是因為它是在先的。
單子在較大與較小之間是均衡、在意向與緩解之間是中間、在眾多中是居中、在時間中是現在,因為永恆既不知道過去也不知道未來。它還被稱為朱庇特,因為他是眾神之父和首領、維斯塔,因為這是位於宇宙的中間的火焰之家,而且它就像圓中的點一樣不向任何一邊傾斜、形式,因為它劃定範圍、理解及終結,還有愛、和諧與虔誠,因為它是不可分割的。單子的其它象徵名稱還有船、戰車、普羅透斯(一個能夠改變外貌的神祇)、謨涅摩敘涅和多名者(Polyonymous)。
下列這些象徵性名字被賦予了雙數——數字2——因為這時它已經被分割,而且是分割成雙;當數目變成兩個的時候,其中每一個都會與另一個相對:天賦、邪惡、黑暗、不平等、鬆懈、易動不居、勇敢、堅韌、爭辯、物質、相異、眾多與單子之間的劃分、缺陷、無形狀、不確定、模糊、和諧、容忍、根源、思想噴泉的源泉、頂端、法涅斯、意見、謬誤、他異、自卑、衝動、死亡、動作、世代、突變、分裂、經度、增強、組合、融合、厄運、支撐、施加、婚姻、靈魂跟科學。
在他的《數學》中,W・韋恩・韋斯科特就雙數說道:“它又叫做‘大膽者’(Audacity),系因它是最早從神聖太ㄧ那裡脫離出去的數字,就如迦勒底神諭所述,那是脫離了:‘上帝靜默的內殿’。”
由於單子是父親,故雙數就是母親;因此,雙數也與一些女神產生了共通點,例如伊西斯、瑞亞(朱庇特之母)、弗瑞吉亞、呂狄亞、丁迪米妮(庫柏勒)和刻瑞斯;埃拉托(繆思女神之一)、黛安娜,因為月亮是叉狀的、狄克廷娜、維納斯、狄俄涅、塞希里雅、朱諾,因為她是朱庇特的妻子也是他的妹妹,還有墨丘利的母親邁亞。
雖然單子是智慧的象徵,可是雙數卻是無知的象徵,因為它具有分離感——這種感覺正是無知的開端。然而,雙數同時也是智慧之母,畢竟無知——在超越其自身之後——就可以孕育出智慧。畢達哥拉斯學派崇尚單子,但卻鄙視雙數,因為後者象徵著極端。藉著雙數的力量,深淵便能在與天國的對比中創造出來。深淵映照天國,並會幻化為幻象的象徵,下界僅僅是反映著上界。下界又被喚作摩耶(maya)、幻象、大海、虛空(Great Void),它的象徵表示法還有帶著鏡子的波斯賢士。從雙數中又會衍生出爭執與論辯,直到單子又降臨於雙數之間,也就是由救主-上帝重新建立起平衡,祂以數字的形式接納自己,並在兩個代表人類的盜賊中間被釘死在十字架上。
三元組——數字3——這是第一個確實的奇數(單子並不總是被當作一個數字)。這是第一個均衡的統一體;所以畢達哥拉斯才說阿波羅是從三足鼎上發出神諭,並明智地對奠酒提出三次建議。關於三元組的性質亦有幾個關鍵字,它們包括友誼、和平、正義、謹慎、虔誠、節制與美德。下面這些神祇都分享了三元組的原則:薩頓(時間統治者)、勒托、柯納科帕(Cornucopae)、奧菲特(大蛇)、忒提斯、赫卡特、波利海妮婭(繆思女神)、普路托、特里同、海主、特里托格內亞、阿刻羅俄斯和費斯、弗里斯、格瑞斯。這個數字亦享有智慧之名,因為人們籌劃現在、預見未來並受惠於前車之鑒。這就是智慧與理解的緣由。三元組是智慧之數——音樂、幾何和天文,以及天體與塵世的科學。據畢達哥拉斯教導,這個數字結構還司掌著月圓的力量。
三元組的神聖不可侵犯性和它的象徵——三角形——就是單子與雙數的結晶。單子跟雙數分別是神聖之父與偉大之母的象徵,由這兩者組成的三元組因而是雌雄同體,且代表了上帝從祂自身創造出世界,祂的創造性一面總是被三角形象徵。受單子注入的雙數因此展現了成為後代之父母的能力,而雙數就是須彌山的子宮,世界在這個子宮裡被孵化,而且始終以胚胎的形式蘊於其中。
四元組——數字4——被畢達哥拉斯學派奉為始源之數、萬物之根源、自然的源泉和最完美的數字。所有四元組都帶有智性;它們擁有一個自發秩序,環抱著這個世界,正如天府(Empyreum)居於之中。為什麼畢達哥拉斯學派會以四元組來表達上帝的答案可以在畢氏的聖言中找到,上帝在其中就直接被稱為眾數之數(Number of Numbers)。這是因為十,即數字10就是由1、2、3與4構成的。數字4是上帝的象徵,因為它也是頭四個數字的象徵。此外,四元組也是一個星期的中心,介在1和7之間。四元組同時也是第一個幾何結構體。
畢達哥拉斯認為,人的靈魂是以四元組組成,故靈魂擁有思想、科學、觀點及感覺這四種力量。四元組聯繫著所有存有、元素、數字跟細節;凡是任何不依賴於四元組的事物都不得被命名。它是所有事物的本因與創造者,一個清晰明瞭的上帝,天體和可感之善的締造者,據普魯塔克解釋,聖十三角形也被稱為世界(world),或數字36,係由前四個奇數與前四個偶數相加而成:
1 + 3 +5 +7 = 16
2 + 4 +6 +8 = 20
36
被給予四元組的關鍵字有衝動、力量、男子氣概、二元母性(two-mothered)與自然的司鑰者(key keeper of Nature),因為普世法則不可能少得了它。所以它也被稱為和諧與第一深奧原理。下列這些神祇分享了四元組的性質:海克力士、墨丘利、伏爾甘、巴克斯、烏拉妮亞(繆思女神)。三位一體代表了主要原色與主要行星,而四元組則代表次原色與次要行星。從第一個三角形孕育出七個靈魂,這以一個三角形和一個方形的方式來寓意。這些形狀就是這樣形成了共濟會的圍裙。
五元組——數字5——是奇數和偶數的組合(3+2)。希臘人視五角星為光明、健康還有活力的神聖象徵。它也象徵著第五元素——以太——這個元素不受其它較為低劣的元素干擾。它也被稱作均衡,因為它能將完美的數字10分成兩個相等部分。五元組是自然的象徵,當它自身加倍的時候仍總是可以回歸其自身,宛如麥粒從種子的形式誕生,然後通過自然的過程再孕育出下一代麥粒,週而復始。其它數字如果乘以自己只會產生其它數字,但唯有5和6在乘以自己時仍會在最後一位數保留其自身。
五元組代表所有高等和低等的存有,它有時要不被稱作聖者或奧祕的祭司,這是由來自它與靈性以太的關係,神秘實踐藉此得以實現。五元組的關鍵字是和解、交替、婚姻、不朽、真摯、天意與聲音。分享有五元組性質的神祇包括帕拉斯、涅墨西斯、布巴斯提(巴斯特)、維納斯、安德羅尼亞、塞希里雅以及朱庇特的信使們。
四元組(元素)加上單子後就會變成五元組。按畢達哥拉斯學派的教導,在土、火、氣和水元素裡都還摻入了一種叫做以太的物質——它是活力與生命的基礎。因此,它們才選擇以五角星或五芒星來當作活力、健康和互相貫通的象徵。
哲學家向來習慣以龍的象徵圖像來掩蓋土元素,而且有許多古代英雄都被告知說他們的使命就是要屠龍。因此,他們將自己的劍(單子)插進了龍(四元組)的身體中。這就使得五元組隨之形成,也是精神本質始終勝過物質本質的隱喻。四元素在早期的《聖經》文本裡被象徵性地以從伊甸園流出的四條河來表現,而且這些元素亦都處在〈以西結書〉中的複合物基路伯的掌管之下。
畢達哥拉斯學派主張六元組——數字6——如同亞歷山卓的革利免所指出,是世界的創造的象徵,過往的先知與古代神秘學派亦是如此確信。它於是被畢達哥拉斯學派取作所有部分的完美,這個數字對俄耳甫斯而言尤其神聖,當然對費特、拉刻西斯、繆思和塔利亞也是。它又被稱為形式的形式、宇宙的聲音與靈魂的創造者。
在希臘人眼裡,和諧與靈魂被認為在本質上相似,因為所有靈魂都是和諧的。六元組還是婚姻的象徵,這是由於它乃是被兩個三角形構成,其中一個代表男性另一個代表女性。這些關鍵字都是給予六元組的:時間,因為它是長短的衡量標準、萬靈丹,因為健康就是和諧,而且六元組就是一個平衡數、世界,因為這個世界就像六元組一樣,經常被認為是由和諧的對立物構成、全能,因為它的部分足以匹配整體(3+2+1=6)、永存,因為它包含了不朽的元素。
七元組——數字7——被畢達哥拉斯學派稱為“值得尊敬者”。它被認為是宗教之數,因為人就是被七個他應當向其奉獻的天體之靈所主宰。它又名為生命之數,因為人們相信在懷孕週期的第七個月出生的人往往能活命,可是在第八個月出生的人卻要夭折。有位作家還稱呼這個數字為無母的處女密涅瓦,因為它不是出生於母親,而是天父即單子的王冠或頭部。七元組的關鍵字有財富、機會、保護、控制、管轄、判斷、夢境、聲音、音色以及將所有事物引向終結之物。擁有七元組特性的神祇是埃癸斯、奧西里斯、瑪爾斯、克萊奧(繆思)。
很多古代民族都把七元組奉作神聖數字。猶太人的以羅欣據說總共有七位,他們是黎明之靈,常又被稱為主宰行星的大天使。七位大天使連同在其三重方面控制太陽的三個靈魂ㄧ起構成了10,畢達哥拉斯學派的十元組。神秘的畢達哥拉斯學派聖十三角形或四行點圖形是從1一直增加至4,這就是創造階段的象徵。畢達哥拉斯學派的偉大真理就是自然界中的所有事物均可被十元組或數字10再現,這個典故也被共濟會以十根手指頭的不同握手方式,亦即利用兩個人的各五根手指給巧妙地保存了下來。
3(精神、心智與靈魂)和4(世界)之總和即為7,這是人的神秘本質,由三重精神跟四重物質形式聚合而成。這些東西都是以立方體來做象徵,立方體擁有六個面和一個神秘的第七個點。這六個面也都是方位:北、東、南、西、上與下;或是前、後、右、左、上與下;或者是土、火、氣、水、精神與物質。1就置於這些之中間,它是一個直立的人形,從立方體的中心輻射出六個金字塔。由此衍生出了一句偉大的神秘格言:“中心是方位、尺寸和距離之父。”七元組是律法之數,因為它是宇宙法則的立法者,佇立在王座前的七個靈。
八元組——數字8——因為是第一個表示立方體的數字所以具有神聖性,這個形體有八個角,而且是在10之下的唯一一個能分偶數(1-2-4-8-4-2-1)。所以,8可以被分為兩個4、4可以被分為兩個2、2可以被分為兩個1,這就回溯至單子。八元組的關鍵字是愛、忠告、謹慎、律法與便利。擁有其性質的神祇有帕納莫尼亞、瑞亞、庫柏勒、卡德邁亞、丁迪米妮、奧莉卡、涅普頓、泰美斯、歐忒耳珀(繆思)。八元組是一個與希臘的厄琉息斯秘儀和眾卡比洛斯神秘學派頗有淵源的數字,它還有一個名字叫做小聖數,其形式部分是來自於赫耳墨斯神杖上的蜷曲之蛇,另一部分是來自於天體的蛇形運動;不過也有可能是來自於月亮的節點。
九元組——數字9——是奇數的第一個平方(3x3)。它常與失敗跟缺陷相關聯,因為它還缺臨門一腳才能達到完美數字10。它也被叫做人之數,因為人的懷孕週期就是九個月。它的關鍵字是海洋和地平線,對古人來說這些東西都是無邊無界的。九元組是一個沒有邊界的數字,這是基於除了無限的10之外再沒有其它可以超出者。它還有名曰邊界與限制,因為它一攬了所有數字在內。它另有一個稱呼是氣,這是緣故是它圍繞著所有數字就好比空氣圍繞地球,分享其性質的男神和女神有普羅米修斯、伏爾甘、朱庇特的妹妹兼妻子朱諾、佩安、卡里忒斯、特里托格內亞、克里特斯、珀耳塞福涅、亥伯龍、忒耳普西科瑞(繆思女神)。
9被認為是邪惡的,因為它是一個倒過來的6。按照厄琉息斯秘儀的說法,這是意識在出生時所必須途中經過的領域的數目。由於它和精子非常相似,所以9也與生命誕生有關。
十元組——數字10——根據畢達哥拉斯學派是最偉大的數字,非但是因為它是聖十三角形(十個點),還因為它含有所有算術跟和聲比例。畢達哥拉斯曾說,10是數字的本質,所有民族無不同意這點,進而為回溯單子提供可能。十元組也被稱為天國與世界,因為前者涵蓋後者。身為一個完美數字,十元組被畢達哥拉斯學派應用於那些與時間、權力、信仰、必要性和記憶的力量有關的事物。它亦被稱作不倦者,因為它有如上帝一樣不知倦怠。畢達哥拉斯學派為天體予以了十種秩序,它們還表示是十元組使全部的數字得以完美,並令它們自身的奇數與偶數、可動者與不可動者、好與壞等本質可被理解。它們將這股力量與這些神祇相提並論:阿特拉斯(因為他背負著這些數字)、烏拉尼亞、謨涅摩敘涅、太陽、法涅斯、獨一神(One God)。
十進制最早可以被追溯回人們尚且只能使用手指頭算術的時候,這是最原始的計數方式之一,而且仍被許多土著民族沿用至今。



沒有留言:
張貼留言